Logarithms

A logarithm is just another form of an exponent.

$2^3=8lo{g}_{2}8=3$

The logarithm tells you what the exponent is:


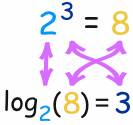
How to do log calculations without calculator.

If you have an unknown value in log form, you first change the equation to exponential form and then solve the unknown value.

$x=lo{g}_{5}2525=5^x{5}^2=5^x\therefore <!--\; \therefore \; -->x=2$

Logs, antilog, log_e and antilog_e a calculator.

Use your calculator '2ndF log' to get antilog and '2ndF IN' to obtain log_e


Log Laws


Law 1

If the base and number are the same the log cancels out and the answer is 1.

log_aa 

= 1

Law 
If you have two logs and their bases are the same, you multiply the numbers.

log_ca + log_cb

= log_cab

Law 3
If you have two logs with the same base and you are subtracting, you divide the numbers.

log_ca - log_cb

= log_c^a/_b

Law 4
If you have a base, number and exponent you write the exponent in front of the log.

log_ab^m

= m log_ab

Law 5
If you have a log with a different base and number you can change the base.

$lo{g}_{a}b=\frac{lo{g}_{c}b}{lo{g}_{c}a}$

Simplify logs without a calculator




Changing the base of a log

Surds

A surd is a value in a root that cannot be determined unless you use a calculator.
Example: √2 (square root of 2) can't be simplified further so it is a surd

How to multiply surds

If you have two surds that are multiplied and their roots are the same, you put them under one root and multiply the values.

$\sqrt{3a}\times <!--\; \times \; -->\sqrt{3a}=\sqrt{3a\times <!--\; \times \; -->3a}=\sqrt{9a^2}=3a$


How to add and subtract surds

If you add and subtract surds, you always have to find a common factor and then simplify the expression.

$2\sqrt{2}+6\sqrt{8}=2\sqrt{2}+6\sqrt{2\times <!--\; \times \; -->4}\text{(write 8 as 2 times 4)}=2\sqrt{2}+6\times <!--\; \times \; -->2\sqrt{2}\text{(the root of 4 is 2)}=2\sqrt{2}+12\sqrt{2}=\sqrt{2}(2+12)\text{(take }\sqrt{2}\text{out as common factor)}=14\sqrt{2}$

Rationalizing denominators 

When fractions have a surd in the denominator we can rationalize the denominator so that it is not in surd form. We do this by multiplication.

Factors 

To simplify an expression you must always try to take out common factors.

$\sqrt{4-<!--\; -\; -->4x}=\sqrt{4(1-<!--\; -\; -->x)}=\sqrt{4}\times <!--\; \times \; -->\sqrt{1-<!--\; -\; -->x}\text{(}\sqrt{4}=2)=2\sqrt{1-<!--\; -\; -->x}$


Equations with surds 

Given an equation that contains a surd you must always first change the surd into a form that has no root sign and then solve the unknown values.

How to Simplify Radicals/Surds Summery

Exponents

Exponent Laws

Law 1
If you multiply, and the bases are the same you add the exponents.

a ⁿ × a ^m = a ^n+m

Law 2
If you divide, and the bases are the same you subtract the exponents.

a ⁿ ÷ a ^m = a ^n-m

Law 3
If you have an exponent inside a bracket and an exponent outside the bracket, you multiply the exponents.

(a ⁿ )^m = a ^nm

Law 4
Anything except zero to the power of zero is one.

a ⁰ = 1

Law 5
If you have a negative exponent and you want to make it positive, you change the value inside the bracket around. Only the sign of the exponent changes.

(a)^{-m = (1/a)m}

Law 6
If you have a fraction as an exponent you change it to root form. The denominator will then be the root.
$a^{\frac{m}{n}}=\sqrt[n]{a^m}$


Exponential equations

Algebraic Fractions

Simplification of fractions

Multiplication of fractions

Note 1: When you divide two fractions, you turn the fraction after the division sign around, and then you change the sign to a multiplication.

Note 2: Remember that you can only cancel out if there is a multiplication or division sign between terms.

How to add and subtract fractions

Cube Fractions

Function notation

Functional notation is the notation for expressing functions as  


Function values

You use function values when a value for x is given and you are asked to solve an equation. To solve the equation, you put x's value into each x in the equation.

The remainder theorem - using long division

The factor theorem

You use the factor theorem as an easy way to find out whether a term is a factor of an equation, without doing long division:

Squares

Difference between two squares

Method for completing the square

The quadratic formula

${\displaystyle x=\frac{-<!--\; -\; -->b\pm <!--\; \pm \; -->{\displaystyle \sqrt{b^2-<!--\; -\; -->4ac}}}{2a}\text{when}a{x}^2+bx+c=0}$

Solve Quadratic Trinomials

The general form for a quadratic trinomial is:

$a{x}^2+bx+c$

Check out this video how to solve them:

Here is another method:

Also remember:

• If the sign of the third term is positive, then the signs of the factors will be the same.
• If the sign of the third term is negative, the signs of the factors will be different.

The highest common factor HCF

When it has been a few years since you last done some math, this video is excellent to refresh you memory, you will be able to get the highest common factor easily after this:

Operations and understanding the Vocabulary of Algebra

Operations

$+\times <!--\; \times \; -->+=+-<!--\; -\; -->\times <!--\; \times \; -->-<!--\; -\; -->=++\times <!--\; \times \; -->-<!--\; -\; -->=-<!--\; -\; -->-<!--\; -\; -->\times <!--\; \times \; -->+=-<!--\; -\; -->$
When they occur in same sentence; first \(\times\) then \(\div\) then + then -. Always left to right.

Understanding the Vocabulary of Algebra

What is a prime number?

List of prime numbers