http://www.cymath.com/
http://www.mathportal.org/calculators.php
https://www.desmos.com/calculator
Wednesday, October 1, 2014
Tuesday, September 30, 2014
Sketch graphs of trigonometric functions
Graphs of sin θ, cos θ and tan θ
Remember sin graph starts at 0
Amplitude and period transformations
Solving triangles
Right Angled Triangles
Sine Rule
Determine the sides
Determine the angles
Cosine Rule
Determine the sides
Determine the angles
Trig Ratios
30°, 45° and 60°
45°, 45°, 90°
When you work with trig and radians, π means the same as 180° because 2π radians is a full circle 360°
Trig Ratios for positive multiples of
30°, 45° and 60°
Negative Multiples of 30°, 60° and 45° trig ratios
Reduction Formulae
Trigonometric identities
Identities
Proving trigonometric identities
Solving trigonometric equations using identities
Proving trigonometric identities
Solving trigonometric equations using identities
Monday, September 29, 2014
Trigonometric equations
Using CAST
Equations with multiple angles
Trigonometric equations that factorise
Solving a trigonometric equation by using reciprocal function
Make everything sin and cos
Equations with multiple angles
Trigonometric equations that factorise
Solving a trigonometric equation by using reciprocal function
Make everything sin and cos
Thursday, September 25, 2014
Trigonometric functions
Basic Trigonometry: Sin, Cos, Tan
Relation between the trigonometric functions

Relation between the trigonometric functions

Differential Calculus
Average gradient
Change in yChange in x
=△y△x
=y2−y1x2−x1


Limits
Limits from first principles
Differentiation
Differentiate from first principles
Rules of differentiation
Notation
The gradient of a curve
Turning points


Limits
Limits from first principles
Differentiation
Differentiate from first principles
Rules of differentiation
Notation
The gradient of a curve
Turning points
Monday, September 22, 2014
Intro to Differential Calculus
Functional notation, average gradient, limits, derivative from first principles and rules
Thursday, September 18, 2014
Sketch graphs
Straight line
You can also let y=0 and calculate x to draw the line.
The Circle
The Ellipse
The Parabola
The Hyperbola
Solve simultaneous equations graphically
You can also let y=0 and calculate x to draw the line.
The Circle
The Ellipse
The Parabola
The Hyperbola
Solve simultaneous equations graphically
Tuesday, September 16, 2014
Monday, September 15, 2014
Equations of straight lines
Two point form

One point and a gradient (Point slope form)
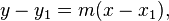
The distance between two points
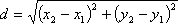 ,
,
The midpoint of a line segment
![[(x_1 + x_2)/2 , (y_1 + y_2)/2]](http://www.purplemath.com/modules/xyplane/midpt07.gif) ,
,

One point and a gradient (Point slope form)
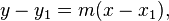
The distance between two points
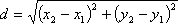 ,
,The midpoint of a line segment
![[(x_1 + x_2)/2 , (y_1 + y_2)/2]](http://www.purplemath.com/modules/xyplane/midpt07.gif) ,
,Tuesday, September 9, 2014
Different forms of the Straight line
The Gradient(Slope)-intercept form
Where m = gradient = difference in y divided by the difference in x
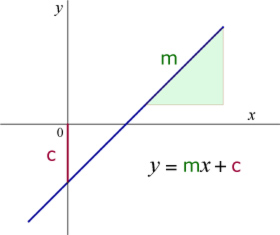
The Intercept form


http://www.vitutor.com/geometry/line/intercept_form.html
The General form
Angle between points is given
If you are given an angle (Θ) and you must determine the gradient: The tangent of the angle is the gradient of the line: tanΘ = m
The equation is given
m is the gradient.
Two points are given
Parallel lines
If two lines are parallel, their gradients are the same.
Perpendicular lines
If two lines are perpendicular, their gradients are opposite and inverse of one another.
Where m = gradient = difference in y divided by the difference in x
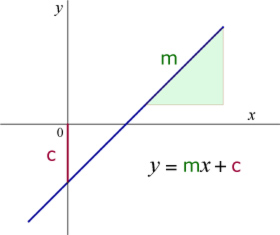
The Intercept form


http://www.vitutor.com/geometry/line/intercept_form.html
The General form
Angle between points is given
If you are given an angle (Θ) and you must determine the gradient: The tangent of the angle is the gradient of the line: tanΘ = m
The equation is given
m is the gradient.
Two points are given
Parallel lines
If two lines are parallel, their gradients are the same.
Perpendicular lines
If two lines are perpendicular, their gradients are opposite and inverse of one another.
Monday, September 8, 2014
Manipulation of technical formulee
Rules for manipulating formulas
- What you do on the one side of the equal sign you must do on the other side.
- If you must make an exponent the subject, you use logs.
- The inverse operation of a 'root' is a 'power'.
Thursday, September 4, 2014
Tuesday, September 2, 2014
Linear equations
Linear equations
If the variable occurs more than once first simplify. The variables must all be taken to one side and then added or subtracted.
If the variable occurs in the denominator of a fraction, it must be removed. This is done by multiplying by the variable throughout the equation.
Simultaneous linear equations
Solving simultaneous equations (one linear and one quadratic)
If the variable occurs more than once first simplify. The variables must all be taken to one side and then added or subtracted.
If the variable occurs in the denominator of a fraction, it must be removed. This is done by multiplying by the variable throughout the equation.
Simultaneous linear equations
Solving simultaneous equations (one linear and one quadratic)
Friday, August 29, 2014
Logarithms
A logarithm is just another form of an exponent.
The logarithm tells you what the exponent is:
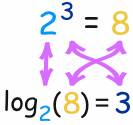
How to do log calculations without calculator.
If you have an unknown value in log form, you first change the equation to exponential form and then solve the unknown value.
Logs, antilog, loge and antiloge a calculator.
Use your calculator '2ndF log' to get antilog and '2ndF IN' to obtain loge
Log Laws
Law 1
= 1
Law
If you have two logs and their bases are the same, you multiply the numbers.
Simplify logs without a calculator
Changing the base of a log
The logarithm tells you what the exponent is:
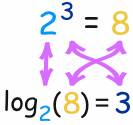
How to do log calculations without calculator.
If you have an unknown value in log form, you first change the equation to exponential form and then solve the unknown value.
Logs, antilog, loge and antiloge a calculator.
Use your calculator '2ndF log' to get antilog and '2ndF IN' to obtain loge
Log Laws
Law 1
If the base and number are the same the log cancels out and the answer is 1.
logaa
Law
If you have two logs and their bases are the same, you multiply the numbers.
logca + logcb
= logcab
Law 3
If you have two logs with the same base and you are subtracting, you divide the numbers.
If you have two logs with the same base and you are subtracting, you divide the numbers.
logca - logcb
= logca/b
Law 4
If you have a base, number and exponent you write the exponent in front of the log.
If you have a base, number and exponent you write the exponent in front of the log.
logab
= m logab
Law 5
If you have a log with a different base and number you can change the base.
If you have a log with a different base and number you can change the base.
Simplify logs without a calculator
Changing the base of a log
Thursday, August 28, 2014
Surds
A surd is a value in a root that cannot be determined unless you use a calculator.
Example: √2 (square root of 2) can't be simplified further so it is a surd
How to multiply surds
If you have two surds that are multiplied and their roots are the same, you put them under one root and multiply the values.
How to add and subtract surds
If you add and subtract surds, you always have to find a common factor and then simplify the expression.
Rationalizing denominators
When fractions have a surd in the denominator we can rationalize the denominator so that it is not in surd form. We do this by multiplication.
Factors
To simplify an expression you must always try to take out common factors.
Equations with surds
Given an equation that contains a surd you must always first change the surd into a form that has no root sign and then solve the unknown values.
Example: √2 (square root of 2) can't be simplified further so it is a surd
How to multiply surds
If you have two surds that are multiplied and their roots are the same, you put them under one root and multiply the values.
How to add and subtract surds
If you add and subtract surds, you always have to find a common factor and then simplify the expression.
Rationalizing denominators
When fractions have a surd in the denominator we can rationalize the denominator so that it is not in surd form. We do this by multiplication.
Factors
To simplify an expression you must always try to take out common factors.
Equations with surds
Given an equation that contains a surd you must always first change the surd into a form that has no root sign and then solve the unknown values.
How to Simplify Radicals/Surds Summery
Wednesday, August 27, 2014
Exponents
Exponent Laws
Law 1
If you multiply, and the bases are the same you add the exponents.
Law 2
If you divide, and the bases are the same you subtract the exponents.
Law 3
If you have an exponent inside a bracket and an exponent outside the bracket, you multiply the exponents.
Law 4
Anything except zero to the power of zero is one.
Law 5
If you have a negative exponent and you want to make it positive, you change the value inside the bracket around. Only the sign of the exponent changes.
Law 1
If you multiply, and the bases are the same you add the exponents.
a n × a m = a n+m
If you divide, and the bases are the same you subtract the exponents.
a n ÷ a m = a n-m
If you have an exponent inside a bracket and an exponent outside the bracket, you multiply the exponents.
(a n )m = a nm
Anything except zero to the power of zero is one.
a 0 = 1
If you have a negative exponent and you want to make it positive, you change the value inside the bracket around. Only the sign of the exponent changes.
(a)-m = (1/a)m
Law 6
If you have a fraction as an exponent you change it to root form. The denominator will then be the root.
Exponential equations
If you have a fraction as an exponent you change it to root form. The denominator will then be the root.
Exponential equations
Thursday, August 21, 2014
Algebraic Fractions
Simplification of fractions
Multiplication of fractions
Note 1: When you divide two fractions, you turn the fraction after the division sign around, and then you change the sign to a multiplication.
Note 2: Remember that you can only cancel out if there is a multiplication or division sign between terms.
How to add and subtract fractions
Multiplication of fractions
Note 1: When you divide two fractions, you turn the fraction after the division sign around, and then you change the sign to a multiplication.
Note 2: Remember that you can only cancel out if there is a multiplication or division sign between terms.
How to add and subtract fractions
Wednesday, August 20, 2014
Cube Fractions
Function notation
Functional notation is the notation for expressing functions as

Function values
You use function values when a value for x is given and you are asked to solve an equation. To solve the equation, you put x's value into each x in the equation.
The remainder theorem - using long division
The factor theorem
You use the factor theorem as an easy way to find out whether a term is a factor of an equation, without doing long division:
Functional notation is the notation for expressing functions as


Function values
You use function values when a value for x is given and you are asked to solve an equation. To solve the equation, you put x's value into each x in the equation.
The remainder theorem - using long division
The factor theorem
You use the factor theorem as an easy way to find out whether a term is a factor of an equation, without doing long division:
Subscribe to:
Comments (Atom)